Ana Cláudia Pereira, Graziane Sales Teodoro, Ricardo Edem Ferreira, Helvécio G. F. Filho
Professores do Instituto de Ciências Exatas (ICE)
Nos últimos meses, muito se tem ouvido falar a respeito do aumento do número de casos do novo coronavírus. E, em meio a tantas notícias sobre a pandemia, a expressão “crescimento exponencial” tornou-se bastante comum. Como todas as reportagens mostram, a expressão crescimento exponencial refere-se a um aumento acentuado no número de casos. Mas de onde vem essa expressão?
No ensino médio, estudamos uma função chamada função exponencial, que apresenta um crescimento ou decrescimento muito rápido. Ela pode ser identificada em situações do dia a dia, tais como problemas envolvendo crescimento de um capital aplicado à taxa de juros compostos, decaimento radioativo, crescimento de bactérias em uma colônia, resfriamento de um corpo, crescimento populacional e, atualmente, é muito utilizada para descrever o crescimento de pessoas infectadas pelo coronavírus.
Coronavírus é uma família de vírus que causam infecções respiratórias. Em dezembro de 2019, a Organização Mundial da Saúde (OMS) foi alertada sobre vários casos de pessoas infectadas pelo novo coronavírus na China, causador da doença Covid-19. Com o fluxo internacional de pessoas, em pouco tempo o vírus se espalhou para o mundo e alcançou 189 países.
O primeiro caso de coronavírus no Brasil foi registrado no dia 26 de fevereiro de 2020, em São Paulo. O Brasil confirmou 5.140.863 casos e 151.747 mortes até o dia 14 de outubro de 2020 segundo dados fornecidos pelo governo brasileiro (covid.saude.gov.br).
Em epidemias de fácil contágio, como ocorre com o coronavírus, cada pessoa pode transmitir o vírus para diversas outras pessoas. Se toda a população for suscetível ao contágio e se cada infectado contagiar m novos casos em média, sendo m uma constante maior do que 1, o crescimento é exponencial.
Por exemplo, se cada indivíduo infectado transmite a doença para duas pessoas, m=2, temos o seguinte esquema de propagação:
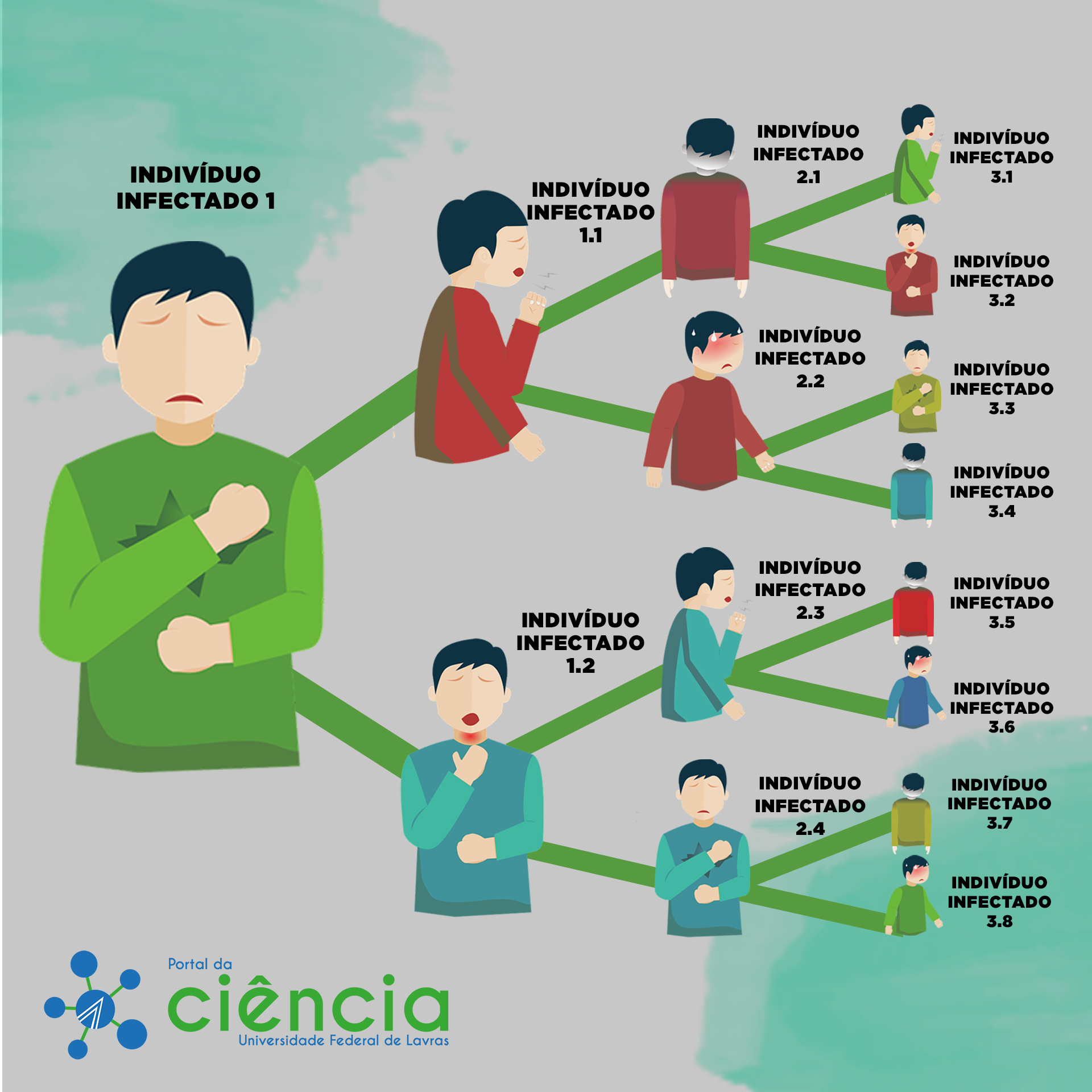
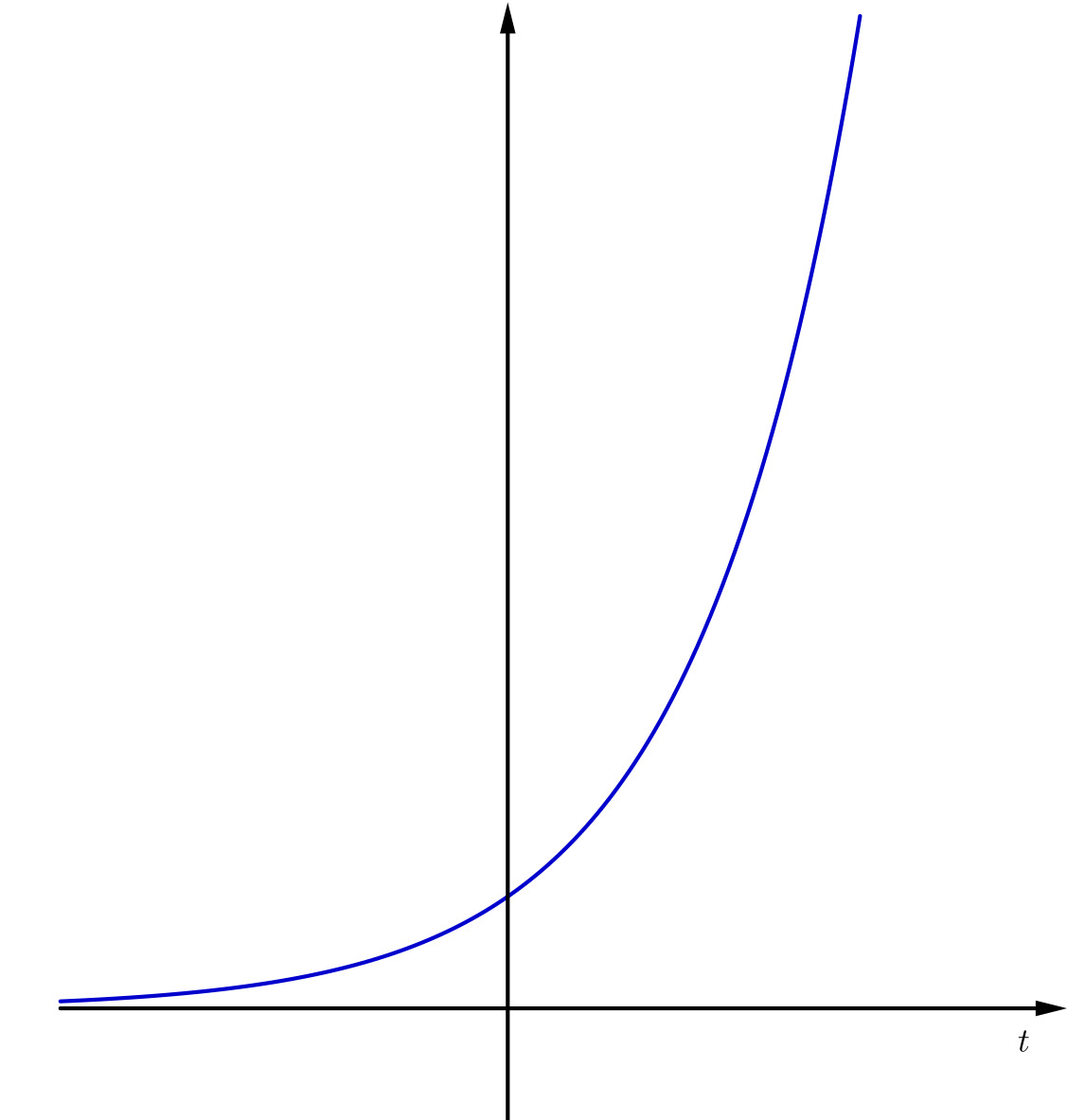
Esquema de propagação da Covid-19 e gráfico da função exponencial
Em notação matemática, o esquema desse exemplo fica f(t)=2t, em que t representa o tempo e f(t), o número de infectados no instante t (Veja o gráfico da função f acima).
Para saber a relação entre o tempo e o número de infectados, os matemáticos propõem modelos matemáticos que têm o objetivo de retratar a situação real.
Um dos primeiros modelos matemáticos acerca de doenças epidemiológicas deve-se a Daniel Bernoulli (1700-1782). Daniel foi o mais famoso dentre os três irmãos, todos pesquisadores matemáticos. Ele contribuiu de forma significativa com as áreas de Física, Astronomia, Probabilidade, Matemática, sendo um pioneiro no campo das Equações Diferenciais Parciais e suas aplicações. Devido às suas contribuições, foi agraciado dez vezes com o Prêmio da Academia de Ciências de Paris.
Em 1760, Daniel Bernoulli propôs e analisou um modelo matemático, a fim de avaliar os efeitos da variolação. A variolação era uma técnica trazida da China, por volta de 1700, considerada o único meio de combater o espalhamento da varíola, que havia se tornado uma das principais causas de morte na Europa Ocidental, no século XVIII.
O modelo proposto por Daniel Bernoulli é composto de duas equações diferenciais, e leva em consideração o número de indivíduos suscetíveis à doença, a população total, a taxa na qual os suscetíveis contraem a doença, a proporção de suscetíveis que morrem em decorrência da doença e a taxa de morte cuja causa não é a doença em questão.
Com esse modelo, ele concluiu que se a varíola fosse eliminada, a vida média da população aumentaria em 3 anos, passando a vida média de 26 anos e meio para quase 30 anos.
Nos últimos séculos, vários pesquisadores do mundo todo têm se proposto a construir modelos cada vez mais elaborados e adequados às doenças que surgem. O modelo utilizado nos estudos da Covid-19, por exemplo, foi proposto em 1927, por W. O. Kermack e A. G. McKendrick, e é conhecido como Modelo SIR. O modelo SIR divide a população em três classes: os suscetíveis, os infectados e os removidos, sendo considerados removidos indivíduos que estão curados ou vierem a óbito. O modelo SIR é adequado para estudar doenças em que indivíduos infectados que sobrevivem adquirem imunidade.
É por meio dos resultados obtidos com os modelos matemáticos que os pesquisadores podem prever a eficiência do isolamento social e de medidas de proteção e a porcentagem de indivíduos que devem ser vacinados para erradicar uma doença. Desse modo, a Matemática ajuda o governo a tomar decisões mais assertivas em relação ao combate ao novo coronavírus.
Os conteúdos e opiniões apresentados nos artigos desta seção são de responsabilidade exclusiva de seus autores, não correspondem à posição institucional da UFLA. As informações, as fotos e os textos podem ser usados e reproduzidos, integral ou parcialmente, desde que a fonte seja devidamente citada e que não haja alteração de sentido em seu conteúdo.
